Как построить выкройку-развертку усеченного овального конуса?

Круглый конус в геометрии

Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.

Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.

Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.

Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.

Технология гибки листового металла своими руками

В процессе строительства дома или дачи зачастую появляется необходимость в оборудовании водостоков, канализации, каркасов из металла.

При изготовлении подобных изделий необходимо придать плоской заготовке необходимую пространственную форму. Советы опытных мастеров, как загнуть лист металла в домашних условиях, позволят изготавливать конструкции хорошего качества, которые прослужат долгое время.

Технология гибки – основные сведения

Сгибание металла выполняют без сварочных швов, что позволяет избежать коррозии в дальнейшем и получить изделие повышенной прочности. Деформация не требует значительных усилий и выполняется, как правило, в холодном состоянии.

Исключение составляют твердые материалы, вроде дюрали или углеродистых сталей. Технология гибки листового металла разрабатывается соответственно поставленным задачам в таких вариантах, как:

• радиусная,
• многоугловая,
• одноугловая,
• п-образная.

Как сделать конус из картона

Вы узнали, как сделать конус из простой бумаги А4, но, если вам нужна плотная поделка, лучше воспользоваться картоном. Материалы и инструменты остаются теми же, что и в предыдущих поделках. Различие заключается только в оттенке картона, его подбираем исходя из предназначения.

Будущий конус будет достаточно прочным за счет чего, его применение может быть широким. Подобную методику работы мы уже рассмотрели выше, но это изготовление все же отличается.

1. Возьмите картон нужного оттенка. Определите середину листа и используя циркуль начертите круг.
2. Полученную окружность нужно разделить на четыре равные доли. Для разделения фигуры на правильные части проведите через полученную ранее точку в центре прямые линии.
3. Складываем круг в разных направлениях. Вы получите четыре сегмента. Один из них нужно вырезать.
4. Полученную заготовку сворачиваем образуя колпак. Так как картон может не сразу склеиться, закрепляем низ фигуры степлером. И только затем промазываем фигуру ПВА.

Плотный конус готов. Если вам нужна не одна геометрическая фигура, а несколько, первый полученный круг, в котором уже вырезана одна четверть, можно использовать в качестве шаблона.

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем

Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

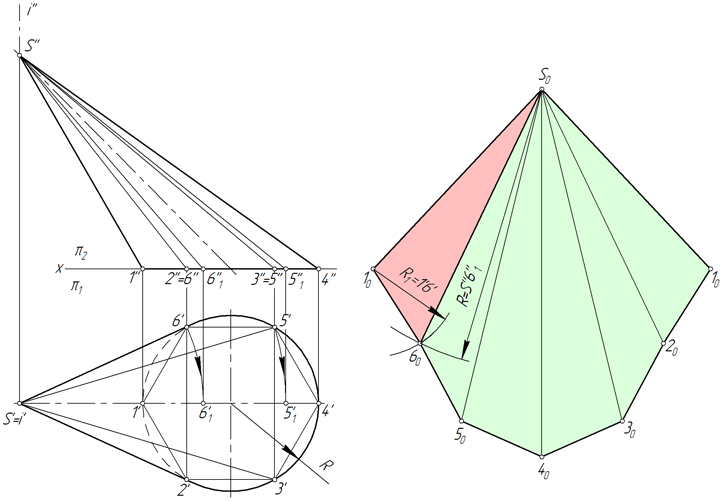
1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’₁, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
4. Соединяем точки A, B, C плавной линией.

Приспособления

Для нанесения резьбы своими руками используют небольшие приспособления:

Выполнены все эти приспособления сплавов, отличающихся повышенной прочностью и стойкостью к истиранию. На их поверхности нанесены желобки и канавки, при помощи которых получается их зеркальное отображение на обрабатываемой детали.

Любой метчик или плашка промаркированы — на них нанесена надпись, обозначающая тип резьбы, которую данное устройство нарезает — диаметр и шаг. Вставляются они в держатели — воротки и плашкодержатели — закрепляются там при помощи винтов. Зажав приспособление для нарезки резьбы в держателе, его надевают/вставляют в то место, где требуется сделать разъемное соединение. Прокручивая устройство, формируют витки. От того, насколько правильно выставлено устройство в начале работы зависит ровно ли «лягут» витки. Потому первые обороты делайте стараясь удерживать конструкцию ровно, не допуская сдвигов и перекосов. После того, как сделано несколько оборотов, процесс пойдет проще.

Вручную можно нарезать резьбу малого или среднего диаметра. Сложные типы (двух- и трехходовые) или работа с большими диаметрами руками невозможна — слишком большие усилия требуются. Для этих целей используется специальное механизированное оборудование — на токарные станки с закрепленными на них метчиками и плашками.

Формула расчета угла конуса

ГОСТ Р 53440-2009(ИСО 1119:1998)

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Основные нормы взаимозаменяемости

ХАРАКТЕРИСТИКИ ИЗДЕЛИЙ ГЕОМЕТРИЧЕСКИЕ

Нормальные конусности и углы конусов

Basic norms of interchangeability. Geometrical product specifications. Standard rates of taper and cone angles

ОКС 17.040ОКСТУ 0074

Дата введения 2012-01-01

Сведения о стандарте

1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский и конструкторский институт средств измерений в машиностроении» (ОАО «НИИизмерения») на основе собственного аутентичного перевода на русский язык стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 242 «Допуски и средства контроля»

4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 1119:1998 «Геометрические характеристики изделий. Ряды конусностей и углов конусов» (ISO 1119:1998 «Geometrical product specifications (GPS) — Series of conical tapers and taper angles», MOD).

При этом в него не включено приложение А (справочное) «Связи в матричной системе GPS» применяемого международного стандарта, которое нецелесообразно применять в национальной стандартизации в связи с тем, что оно содержит сведения о матричной модели Системы стандартов ИСО «Геометрические характеристики изделий (GPS)» и месте применяемого международного стандарта в ней, не относящиеся к объекту стандартизации.

В настоящий стандарт относительно применяемого международного стандарта внесены следующие технические отклонения:

— «Библиография» приведена в соответствие с содержанием стандарта и требованиями ГОСТ Р 1.5-2004.

Указанное приложение, не включенное в настоящий стандарт, приведено в дополнительном приложении ДА.

— ссылки на международные стандарты ИСО заменены ссылками на соответствующие национальные стандарты Российской Федерации согласно таблице А.1 приложения ДБ;

Наименование настоящего стандарта изменено относительно наименования применяемого международного стандарта для приведения в соответствие с требованиями ГОСТ Р 1.5-2004 (пункт 3.5)

5 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет

Уклон и Конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.

Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали.

Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона.

Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах.

Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.

Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Вальцовочные работы по металлу

Вальцовкой называется процесс деформации заготовок из металла с целью приданиям им требуемой формы и размеров. Это могут быть как готовые изделия, так и промежуточные этапы работы с заготовками и элементами. Наиболее востребована вальцовка листового металла и вальцовка труб, она применяется чтобы изменить диаметр, сделать трубу с квадратным или прямоугольным профилем, придать необходимый радиус кривизны, создать изделия овальной, конической, цилиндрической формы.

Обрабатываем:

• Металлические изделия (трубы, профиль, арматура, уголки, обечайки, балки, кольца, конуса, швеллеры)
• Листовому металлу
• Черным металлам (сталь, нержавейка, чугун, железо)
• Цветным металлам, Сплавам (алюминий, медь, латунь, титан)

Колпак на дымоход своими руками – конструкция и чертежи

Через дымоход на улицу выходит смесь газов с продуктами сгорания топлива из каминов, печей и отопительных котлов. Рассматривая частные дома, можно заметить, что оголовок трубы венчает специальный козырек или зонтик.

С первого взгляда на эти приспособления, украшенные фигурной ковкой, затейливыми узорами и фигурками, складывается впечатление, что они всего лишь элемент декора. На самом деле колпак на дымоход является важным элементом системы дымоудаления, правильность конструкции и монтажа которого отражается на эффективности ее работы.

Эта статья расскажет о принципах работы, видах и способах самостоятельного изготовления дефлекторов своими руками.

Как сделать конус для елки своими руками?

Для изготовления такой ели потребуется картон, обычная и цветная бумага, ножницы и клей. И разумеется — побольше фантазии. Наилучший материал для изготовления конуса-основы для ёлки – картон. Только для маленьких нежных и воздушных ёлочек, конус можно делать из бумаги.

Конус сворачивается двумя способами

Лист картона скручивается самым элементарным образом, наподобие кулька для семечек. Лишние края, выступающие из широкой части конуса, обрезаются, а сам конус склеивается. Нижний край обрезается так, чтобы конус стоял ровно и не косился на одну сторону.

На картоне вычерчивается ровный круг (лучше циркулем, но можно обвести тарелку или таз, правда в этом случае трудно будет найти центр) и делится на четыре равные части. Одна из этих частей вырезается, после чего из оставшейся фигуры скручивается конус необходимой сбежистости. Края закрепляются клеем. Конус уравновешивается, аналогично первому способу.

После этого можно делать «хвою» или «ветки» любым выбранным способом, а затем украшать гирляндами лампочек, маленькими игрушками и т.д. Такие ёлочки подходят не только для украшения дома, но и для новогоднего подарка.

Расчет развертки конуса.

Возьмем вертикальную и горизонтальную проекции конуса (рис. 1, а). Вертикальная проекция конуса будет иметь вид треугольника, основание которого равно диаметру окружности, а стороны равны образующей конуса. Горизонтальная проекция конуса будет изображаться окружностью. Если задана высота конуса Н, то длина образующей определяется по формуле:

т. е. как гипотенуза прямоугольного треугольника.

Обвернем картоном поверхность конуса. Развернув картон снова в одну плоскость (рис. 1, б), получим сектор, радиус которого равен длине образующей конуса, а длина дуги равна длине окружности основания конуса. Полную развертку боковой поверхности конуса выполняют следующим образом.

Рис. 1. Развертка конуса:а — проекция; б — развертка.

Угол развертки конуса.

Принимая за радиус образующую конуса (рис. 1, б), на металле вычерчивают дугу, на которой затем откладывают отрезок дуги КМ

, равный длине окружности основания конуса2πr . Длине дуги в2πr соответствует уголα , величина которого определяется по формуле:

г — радиус окружности основания конуса;

l — длина образующей конуса.

Построение развертки сводится к следующему. На длине ранее вычерченной дуги откладывается не часть дуги КМ

, что практически является невозможным, а хорда, соединяющая концы этой дуги и соответствующая углуα . Величина хорды для заданного угла находится в справочнике или проставляется на чертеже.

Найденные точки КМ

соединяются с центром окружности. Круговой сектор, полученный в результате построения, будет развернутой боковой поверхностью конуса.

Получение фигуры с помощью вращения

Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.

Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.

Очевидно, что катет a будет радиусом основания фигуры, катет b — его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.

Основные определения

Прямой круговой конус образован вращением прямоугольного треугольника вокруг одного катета. Как видно, понятие конуса не изменилось со времен Евклида.

Гипотенуза AS прямоугольного треугольника AOS при вращении вокруг катета OS образует боковую поверхность конуса, поэтому называется образующей. Катет OS треугольника превращается одновременно в высоту конуса и его ось. Точка S становится вершиной конуса. Катет AO, описав круг (основание), превратился в радиус конуса.

Если сверху провести плоскость через вершину и ось конуса, то можно увидеть, что полученное осевое сечение представляет собой равнобедренный треугольник, в котором ось является высотой треугольника.

Также часто требуется рассчитать площадь боковой поверхности тела вращения. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.

S=C*L/2=n*R*L/2

где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Что означает уклон в процентах, и как перевести его в градусы

Когда идет речь о кровле зданий, то под словом «уклон» подразумевают угол наклона оболочки крыши к горизонту. В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.

Расчет уклона в процентах

Попробуйте представить прямоугольный треугольник АВС, лежащей на одном из своих катетов АВ. Второй катет ВС будет направлен вертикально вверх, а гипотенуза АС образует с нижним катетом некий угол. Теперь нам предстоит немножко вспомнить тригонометрию и рассчитать его тангенс, который как раз и будет характеризовать уклон, образуемый гипотенузой треугольника с нижним катетом. Предположим, что катет АВ = 100 мм, а высота ВС = 36,4 мм. Тогда тангенс нашего угла будет равен 0,364, что по таблицам соответствует 20˚. Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.

Как понимать угол уклона в процентах?

Если дорожный знак показывает 12%, то это означает, что на каждом километре такого подъема или спуска дорога будет подыматься (опускаться) на 120 метров. Чтобы перевести процентное значение в градусы, нужно попросту вычислить арктангенс этого значения и при необходимости перевести его из радиан в привычные градусы. То же самое касается и строительных чертежей. Если, к примеру, указывается, что угол уклона в процентах равен 1, то это означает, что соотношение одного катета к другому равно 0,01.

Почему не в градусах?

Многих наверняка интересует вопрос: «Зачем для уклона использовать еще какие-то проценты?» Действительно, почему бы просто не обойтись одними градусами. Дело в том, что при любых измерениях всегда имеет место некоторая погрешность. Если в проектной документации станут применять градусы, то неминуемо возникнут сложности с монтажом. Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.

Применение на практике

Предположим, что проект строительства загородного дома предполагает устройство скатной кровли. Требуется проверить ее уклон в процентах и градусах, если известно, что высота конька составляет 3.45 метра, а ширина будущего жилища равна 10 метрам. Так как спереди крыша представляет собой равносторонний треугольник, то ее можно разделить на два прямоугольных треугольника, в которых высота конька будет являться одним из катетов. Второй катет находим, разделив ширину дома пополам. Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan-1(0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.