Гиперкуб

Как нарисовать простой объемный квадрат

Итак, как нарисовать квадрат объемный поэтапно? Это не сложно, наш первый способ нарисовать объемный квадрат будет самым простым. Наша задача на этом этапе придать объем квадрату и нарисовать трехмерную фигуру на плоской поверхности бумаги. Давайте приступим!

Шаг 1: Рисуем квадрат

Начните рисовать объемный квадрат (он же куб) с простого плоского квадрата. Это будет лицевая сторона вашего объемного квадрата.

В этом пошаговом уроке вы наверняка получите хорошую практику по рисованию прямых линий)). Постарайтесь нарисовать все стороны квадрата одинаковой длины и постарайтесь, чтобы все углы квадрата были прямые — ровно 90 градусов.

Шаг 2: Добавьте боковые грани

Добавьте три линии, из двух верхних углов и из нижнего правого угла квадрата. Постарайтесь нарисовать все линии одинаковой длины.

Вы можете «поиграть» с углом, под которым рисуете линии. Здесь мы провели линии примерно под углом 45 градусов. Это дает нам наиболее типичный вид Куба(объемного квадрата), на котором вы можете видеть как верхнюю, так и правую сторону куба.

Но поверните боковые линии немного больше вверх или в сторону и вы получите совершенно другие виды объемного квадрата. Просто убедитесь, что все линии имеют одинаковую длину и одинаковый угол наклона.

Шаг 3: Рисуем задние грани

Последний этап, дорисуйте объемный квадрат, добавив последние два ребра. Они должны быть такой же длины, что и наш первоначальный квадрат. Одно ребро рисуем горизонтально (слева направо), другое вертикально (сверху вниз).

Как склеить куб из бумаги

Куб, это геометрическое тело правильной шестигранной формы. Каждая сторона этой геометрической фигуры имеет форму квадрата. Чтобы изготовить куб из бумаги, надо знать длину одной стороны квадрата. Размеры будущего куба ограничиваются размерами материала, с которым будете работать. В интернете есть готовые шаблоны, но подходят они только к формату А4. И только тем, у кого есть интернет, принтер.

Сделать кубик самостоятельно очень легко. Скорее всего, детки с удовольствием присоединяться к вам, получится совместное творчество.

Какие необходимы материалы

Для работы потребуются следующие материалы:

• Плотный лист картона или бумаги подходящего вам размера.
• Чертежную линейку – треугольник (если ее нет, подойдет обычная).
• Наточенный карандаш.
• Острые ножницы.
• Клей.

Как выбрать клей

При выборе клея ориентируйтесь на толщину исходного материала. Если он тонкий, не рекомендуется использовать ПВА и канцелярский клей. Эти клеевые составы имеют жидкую консистенцию, хорошо впитываются в бумагу. Вследствие этого материал намокает и может пойти «волнами». Со временем ПВА и канцелярский клей желтеют, на бумаге могут проявиться некрасивые пятна.

Клей Момент «Кристалл» имеет прозрачную, не очень жидкую текстуру. Не впитывается в бумагу. Некоторое время после нанесения можно корректировать положение склеиваемых поверхностей. Туба с удобным «носиком» позволяет наносить клей как точечно, так и линиями. Имеет специфический химический запах, однако он довольно быстро выветривается.

Клей-карандаш хорошо склеивает картон и бумагу. Однако картон не должен быть очень тяжелым и плотным. Фаворитами на рынке среди клеев – карандашей являются три марки: Момент, Erich Krause, UHU.

Для работы с бумагой и картоном хорошо подходят клеевые пистолеты. Самые распространенные два типа клеевых пистолетов: это большой, с диаметром стержня 11 мм и маленький с диаметром стержня 7 мм. У маленького тонкий наконечник, что очень удобно для работы с мелкими предметами. Клеевой пистолет работает от электросети. Чтобы он нагрелся, необходимо подождать 3-5 минут.

Клей из клеевого пистолета застывает практически сразу, не дает возможно исправить или переделать что-то. При застывании получается твердый, объемный бугорок. Для склеивания тонкой бумаги лучше не использовать.

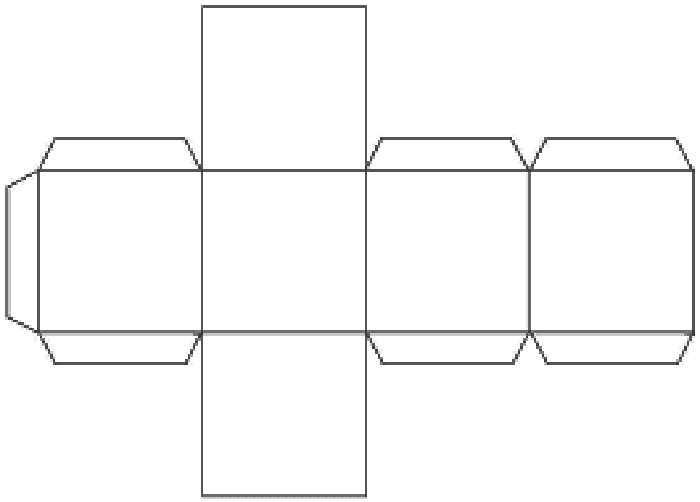
Развёртки геометрических фигур

Большой выбор развёрток простых геометрических фигур.

Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.

Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.

Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.

На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!

Построение куба в перспективе

При построении куба нужно исходить из того, что все его стороны и грани равны. Однако, с визуальной точки зрения все грани куба будут равны только в случае, если он расположен точно перед смотрящим, а обращенная к смотрящему сторона куба точно перпендикулярна его взгляду. Во всех остальных случаях будут иметь место перспективные сокращения.

Учитывая одинаковость всех сторон куба очень важно правильно измерить визуальное направление линий граней куба, их размеры и положение относительно друг друга. Если при замерах будут неточности, которые перекочуют в рисунок, в дальнейшем, при восприятии готового изображения, зритель невольно будет ощущать, что куб имеет не совсем правильные формы

Если куб расположен прямо перед зрителем

Здесь рассмотрим только вариант расположения куба прямо перед зрителем ниже линии горизонта. В этом случае будут видны две стороны куба: фронтальная и верхняя. При учебном рисовании фронтальную сторону можно изобразить в виде обычного квадрата.

Для построения верхней стороны куба требуется нарисовать линию горизонта. Затем на линии горизонта отметить , которая будет расположена точно посередине ранее нарисованного квадрата. Далее следует соединить два верхних угла квадрата с точкой схода. При рисовании с натуры на следующем этапе нужно измерить соотношение высоты видимой фронтальной стороны куба и видимой верхней стороны. Далее это соотношение перенести на рисунок и отметить дальнюю грань верхней стороны куба. После этого провести горизонталь через полученную отметку до линий, уходящих к точке схода. Если рисуется воображаемый куб, то последние описанные выше действия придется делать на глазок, как подсказывает интуиция.

Если куб расположен под углом к зрителю

При расположении куба отличном от точно фронтального, будут видны две или три стороны куба и при построении на линии горизонта образуются . Рассмотрим случай, когда куб расположен ниже линии горизонта под углом к смотрящему. При таком положении куба будут видны три его стороны.

Для начала нужно нарисовать вертикальную линию, которая будет обозначать ближайшую к зрителю грань куба. После этого требуется определить нахождение линии горизонта относительно нарисованной вертикали и отобразить ее. Затем нужно измерить направление исходящих от ближайшей вертикальной грани тех граней, которые сопряжены с ней и уходят в перспективу. После чего следует мысленно перенести направления перспективных граней на рисунок и провести по ним линии от ближайшей вертикальной грани до пересечения их с линией горизонта. Если сделать все правильно, то все грани, уходящие влево от указанной вертикали сойдутся в одной точке схода слева. Те же грани, что визуально уходят вправо сойдутся во второй точке схода на линии горизонта, расположенной справа от первой вертикали.

После этого нужно измерить видимую ширину вертикальных правой и левой сторон куба и на основании замеров провести вертикали, обозначающие дальние вертикальные грани куба. При этом вертикали пересекутся с гранями, уходящими в перспективу. От точек их пересечения с верхними перспективными гранями следует провести линии, уходящие к точкам схода в следующей последовательности: от левой грани к правой точке схода, от правой грани к левой точке схода. При пересечении последних проведенных линий образовался самый дальний от зрителя угол куба.

Из самого дальнего верхнего угла куба проводим вертикаль вниз. Из самого левого нижнего угла проводим линию в точку схода справа, из правого угла в левую точку схода. Последние две линии в идеале должны пересечься между собой в том же месте, где они пересекаются с последней проведенной вниз вертикалью. С помощью построений из этого абзаца построены невидимые грани куба. Они дают понимание устройства куба, что пригодится при дальнейшем рисовании.

Очень важное замечание! Часто при построении более одной точки схода они могут располагаться за пределами рисунка. В этом случае их можно дорисовывать прямо на поверхности, на которой расположен лист с рисунком, либо мысленно достраивать, запоминая их расположение в пространстве для дальнейших построений

Виды штриховки

Перед тем, как мы начнем штриховать куб, вкратце расскажу о том, как техники нанесения линий существуют. Так сложилось, что художники люди творческие и следовать четким правилам им не свойственно, поэтому нет конкретного материала, в котором бы черным по белому были описаны техники штрихования. Однако несколько техник все же используются чаще других, что делает их самыми популярными и основными, среди них:

• Параллельная;
• Перекрестная;
• По контуру;
• Точечная.

В подробном рассмотрении затрону лишь те техники, которые могут пригодиться для штриховки куба.

Параллельная

Состоит из параллельных линий горизонтального или вертикального положения, толщину линий, расстояние между ними и количество слоев индивидуальны. Зависят от того, какая цель перед художником.

Перекрестная

Параллельные вертикальные и горизонтальные линии перекрывают друг друга, образовывая данный подход. Не рекомендуется прямые горизонтальные линии, перекрывать прямыми вертикальными и наоборот, чтобы не создать эффект решетки. Линии должны быть под наклоном, даже если наклон минимальный.

Точечная

По названию не сложно догадаться, что штриховка происходит с помощью точек, расположенных рядом друг c другом. Плотность и количество слоев на ваше усмотрение.

Калькулятор

В интернете встречается большое количество различных калькуляторов, которые могут использоваться для вычисления кубатуры. Большинство вариантов работают на основе простых формул, при написании других применяются сложные логарифмы. В подобном случае расчеты просты:

1. Открывается сайт с онлайн-калькулятором. Их довольно много, разница заключается в количестве вводимых переменных и оформлением. Точность расчетов высокая, но при применении калькулятора в строительстве рекомендуют брать полученный результат с запасом.
2. Выбирается определенное изделие. Это делается для расчета веса и других параметров, так как от типа материала зависит плотность.
3. Указываются другие требуемые параметры.

Формирование куба из бумажных модулей

Используются и другие варианты заготовки для сборки куба – стандартный и шестигранный.

Стандартная фигура

Здесь требуется воспользоваться представленной далее разверткой и последовательностью действий:

Заготовка для куба

1Распечатать или нарисовать самостоятельно развертку на бумаге или картоне. Дополнительно можно нарисовать на заготовке необходимые элементы для украшения фигуры.

2Заготовку требуется вырезать в соответствии с внешними краями.

3Прибавки, которые размещены только в трех квадратах, необходимо прогнуть вовнутрь.

4Далее согнуть грани будущей фигуры не заготовке. Таким образом формируется куб, используемый в дальнейшем.

5Приклеить выступы к квадратам.

Рекомендуется обклеивать фигуру скотчем или другими элементами, которые будут удерживать собранную заготовку и продлят время существования изделия. Лучше делать фигуры сразу из картона – на него можно клеить предварительно развертку и вырезать заготовку уже многослойную.

Можно воспользоваться дополнительной заготовкой, которая немного упростит процесс сборки фигуры. В образце указаны места склеивания, поэтому вся процедура не затребует времени, а новичок в делах со склеиванием элементарных фигур быстро разберется в работе.

Подробная развертка для фигуры

Шестигранная фигура для 12 сторон

Заготовка шестигранника

Требуется выполнить следующую последовательность действий:

1Распечатать или начертить самостоятельно заготовку. Для этого следуют представленному расположению сторон, но используют требуемую длину граней.

2Вырезать заготовку по внешнему краю фигуры.

3Загнуть во внутрь прибавки, чтобы получилась основа для формирования фигуры.

4По линиям расположения граней делают сгибы вовнутрь – получается стандартный шестигранник.

5Основы приклеиваются к сторонам шестигранника.

Пользуются таким шестигранником в играх и изучении различных фигур. Поэтому рекомендуется сделать сразу несколько заготовок и шестигранников, чтобы с детьми было проще изучать первые числа, формы, цвета.

Правила накладывания штрихов

Существуют правила, которые помогают добиться желаемого результата и сделать штриховку красивой. Если им следовать получится быстрее освоить техники и перейти к сложным изображениям.

• Штрихи нужно наносить от тени к свету. У всех предметов есть темные и светлые участки, на которые нужно смотреть при рисовании. Штрихи нужно наносить плавно, от темного к светлому.
• Не объединяйте перекрестную штриховку и растушевку. Могут появиться темные пятна, больше похожие на грязь или случайный мазок рукой.
• При заполнении большого участка, не пытайтесь одним штрихом охватить всю длину или ширину, рисуйте комфортными по длине штрихами.
• Штрихуя последующие слои пытайтесь не попадать на линии, накладывайте штрихи посередине предыдущих.

Ребра – измерения

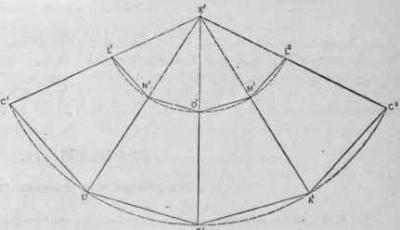
Поясняю, что я называю ребрами-измерениями. Итак, (см. рис. 1.1) в каждой 3ПГК-n
автор определил две «исходные» правильные n-угольные пирамиды:
верхнюю «исходную» пирамиду с вершиной +S, расположенную в первом
«ярусе» между параллельными плоскостями Р_I и Р_II, и нижнюю
«исходную» пирамиду с вершиной –S, расположенную в последнем, n-
«ярусе», между параллельными плоскостями Р_n и Р_n+I.

Боковые ребра этих двух «исходных» пирамид назовем ребрами-измерениями.
Если принять направления в пространстве n ребер-измерений, исходящих из вершины +S
верхней пирамиды, положительно направленными ребрами-измерениями (+),
то, соответственно, n ребер-измерений, исходящих из вершины –S нижней пирамиды,
надо считать отрицательно направленными ребрами-измерениями (-). – Это с одной стороны.

А с другой стороны: ребра-измерения имеют свою векторную направленность
относительно именно данной рассматриваемой вершины в 3ПГК-n.

Поясняю, как я это понимаю: любое ребро в 3ПГК-n соединяет две вершины 3ПГК-n; если для одной из этих
двух вершин это ребро является положительным ребром-вектором, то для второй
вершины (или относительно второй вершины) это же ребро является отрицательным
ребром-вектором. Все в Мироздании относительно. Все познается в
сравнении.

Поэтому, когда вы начертите горизонтальную проекцию «исходной» правильной
n-угольной пирамиды с вершиной в точке +S, вы должны мысленно или на чертеже сразу
же обозначить (начертить) противоположные ребра-измерения нижней «исходной»
пирамиды с вершиной в точке –S.

Обратим особое внимание на следующее:

1) в 3ПГК-n, где n – четное число (т.е. n = 4, 6, 8, 10, …), основания
«исходных» пирамид (т.е. правильные n-угольники) геометрически зеркальны,
то есть при строго вертикальном совмещении этих двух правильных n-угольников
их вершины и ребра совместятся.

В этом случае горизонтальная проекция двух «исходных» пирамид
(введем аббревиатуру: ГП 2ИП-n ) на чертеже (см. рис. 3.13) представлена
в виде n ребер-измерений, но каждое из этих n ребер-измерений содержит
в себе два ребра-измерения различных между собою по знаку;

2) в 3ПГК-n, где n – нечетное число (т.е. n = 3, 5, 7, 9, …), при строго
вертикальном совмещении оснований верхней и нижней «исходных» пирамид —
и вершины, и, соответственно, ребра этих правильных n-угольников геометрически
не совмещены. В этом случае горизонтальная проекция двух «исходных» пирамид
(ГП2ИП-n) на чертеже представлена в виде 2n ребер-измерений, где n
ребер-измерений являются положительными векторами-измерениями и, соответственно,
другие n ребер-измерений являются отрицательными векторами измерениями.

Вот поэтому в первом случае, когда n равно четному числу (n = 4, 6, 8, 10, …),
в самих гиперкубах-n (ГК-n) и в их 3ПГК-n образуются реальные геометрически
совмещенные вершины, и в любой проекции, в любом ракурсе, на всех чертежах
именно эти вершины будут всегда совмещены.

Во втором случае, когда n равно нечетному числу (n = 3, 5, 7, 9, …), в самих
гиперкубах-n (ГК-n) и в их 3ПГК-n нет ни одной геометрически совмещенной вершины,
в горизонтальной проекции совмещены только две вершины: +S и –S, но это –
визуальное совмещение, необходимое при построении именно этой проекции.
В зависимости от выбранного ракурса изображения можно достичь на чертежах
много визуально совмещенных вершин, даже ребер, граней и кубов, но это будет
лишь визуальное совмещение.

Шаг 4 — Проверка пропорций

Для того, чтобы проверить пропорции, закройте один глаз, возьмите карандаш и на вытянутой руке сопоставьте его кончик с верхом переднего ребра куба. Большой палец передвиньте в то место, где ребро заканчивается.

Высота ребра найдена. Теперь, не переставляя палец, наклоните кисть руки на 90 градусов и уже по горизонтали сопоставьте величину одного ребра с другим. Таким образом вы можете проверять и другие величины.

С опытом художники измеряют пропорции «на глаз», это значит, что они обходятся без метода визирования. Их глаз настолько натренирован, что видит размеры без измерений.

Итак, линейное построение подошло к концу, а значит, мы переходим к воздушной перспективе или, проще говоря, к штрихованию.

Светотеневой рисунок куба

Усиление линейного рисунка

Прежде чем наносить светотени усилим линейный рисунок куба за счет увеличения толщин линий и их контрастности. Чем ближе к зрителю расположена грань куба, тем следует сделать ее более толстой и контрастной. Соответственно, чем дальше расположена грань, тем она должна быть менее заметна на рисунке.

Построение теней

На этом этапе . Причем именно построим. Для этого определим местоположение источника света относительно куба и обозначим его на рисунке. Если источник света естественный (Солнце), то проводим вертикаль от источника света до линии горизонта. Если источник света искусственный, то проводим вертикаль от источника света до поверхности, на которой расположен куб.

Затем от источника света проводим лучи через верхние углы куба. После чего, от нижней точки вертикали, опущенной от источника света, проводим лучи через нижние грани куба до пересечения с лучами, проходящими от источника света через верхние углы куба. Ставим точки в местах пересечения верхних и нижних лучей. Теперь соединяем полученные точки между собой и с нижними углами куба. Таким образом получается контур падающей тени.

Собственная тень на кубе определяется визуально. Как правило, собственная тень расположена на предмете с противоположной стороны от источника освещения. Исключением из этого правила являются случаи, когда источников освещения несколько и они расположены с различных сторон от изображаемого предмет. Но, в последнем случае и падающих теней будет несколько.

Тональный рисунок куба

В академическом рисунке тон следует наносить аккуратными штрихами по форме предмета. Мы же допускаем нанесение тона в свободной манере, как штрихами по форме предмета, так и по направлению световых потоков, и даже под любым желаемым углом. Главное, правильно распределить тональные пятна. Начнем с того, что нанесем на всю поверхность тени легкий тон. Далее усилим тени у граней, граничащих с осветленными сторонами куба. После этого еще более усилим те части теней, которые расположены ближе к зрителю.

При всех перечисленных манипуляциях с тоном следует следить за общей тональностью куба и окружающей его обстановки. Если куб выполнен из белого гипса, то и на рисунке он должен выглядеть белым относительно своего окружения

Очень важно не впасть в крайность, при которой в погоне за контрастами и перепадами светотени, однотонный предмет может на рисунке оказаться практически черно-белым

Далее следует усложнить рисунок за счет бликов и рефлексов. Блики на кубе должны оказаться самым светлым местом на рисунке. В тени самыми светлыми местами должны стать рефлексы

Теперь обратим внимание на падающие тени. Как правило, они более контрастные и темные ближе к предмету, от которого образовались

Чем дальше от него, тем границы становятся более размытыми, а тон легким. И в завершении следует добавить тон на фон вокруг куба. Именно фон оттенит освещенные его грани и создаст иллюзию световоздушной среды в рисунке.

Главные принципы и особенности строения трехмерных проекций n-мерных гиперкубов

Прежде чем приступить к построению (черчению) трехмерных проекций n-мерных гиперкубов,
оговорим некоторые закономерности, особенности, главные принципы строения этих геометрических фигур.

Предлагаю вашему вниманию главные геометрические свойства и особенности трехмерных проекций
всех n-мерных гиперкубов (3ПГК-n) и разработанные принципы, методы, правила создания,
построения и черчения трехмерных проекций n-мерных гиперкубов (3ПГК-n).

1. Во всех n-мерных гиперкубах, а также и в их трехмерных проекциях, в каждой вершине сходятся по n ребер.
То есть: в каждой из 16-ти вершин 3ПГК-4 сходятся по 4 ребра, в каждой из 32-х вершин 3ПГК-5
сходятся по 5 ребер, в каждой из 64-х вершин 3ПГК-6 сходятся по 6 ребер, и т.д.

2. Во всех трехмерных проекциях n-мерных гиперкубов (см. рис. 1.1)
в первом «ярусе» (то есть между параллельными плоскостями Р_I и Р_II)
и в последнем «ярусе» (между параллельными плоскостями Р_n и Р_n+I)
находятся по n ребер, сходящихся в верхней вершине, расположенной в плоскости РI, и в нижней вершине,
расположенной в плоскости Рn+I.

Эти n ребер можно (и нужно) представить как боковые ребра правильной n-угольной пирамиды.
Эти пирамиды назовем «исходными» пирамидами.

Вот это и есть очень важная (главная) для построения и черчения трехмерных проекций
n-мерных гиперкубов особенность:

а) в любой 3ПГК-n в первом и в последнем «ярусах» заключена часть тела 3ПГК-n
в виде правильной n-угольной пирамиды;

б) по построенной «исходной» правильной n-угольной пирамиде в любом
ракурсе, в любой проекции можно построить (начертить) и 3ПГК-n в выбранных ракурсах и проекциях.

3. Любое ребро n-мерного гиперкуба (ГК-n), а также его трехмерной проекции (3ПГК-n)
геометрически равно по длине и параллельно одному из n боковых ребер т.н. «исходной»
правильной n-угольной пирамиды, расположенной в первом или последнем «ярусе» ГК-n или 3ПГК-n.

4. Отрезок прямой в теле 3ПГК-n, соединяющий вершины, расположенные в параллельных плоскостях
Р_I и Р_n+I, т.е. вершины верхней и нижней «исходных» правильных
n-угольных пирамид (см. рис. 1.1), перпендикулярен этим плоскостям Р_I и Р_n+I
и является главной осью симметрии 3ПГК-n.

5. В n-мерных гиперкубах, где n – четное число, а также в их трехмерных проекциях
(т.е. в 3ПГК-4, 3ПГК-6, 3ПГК-8, 3ПГК-10, и т.д.), обязательно существуют
геометрически обусловленные совмещенные (сдвоенные) вершины, расположенные в точках
пересечения визуально проведенной главной оси симметрии 3ПГК-n с визуально обозначенными на
рис. 1.1 параллельными плоскостями: Р_III — в 3ПГК-4; Р_III и
Р_V — в 3ПГК-6; Р_III , Р_V и Р_VII — в 3ПГК-8, и т.д.

В этих геометрически обусловленных совмещенных (сдвоенных) вершинах 3ПГК-n соответственно
сходятся по 2n ребер, вот почему я написала фразу: «… в большинстве случаев избежать
совмещения вершин и ребер практически невозможно».

6. При изображении 3ПГК-n (черчении или фотографировании их моделей) в разных ракурсах возможны
визуальные совмещения любых вершин, а также визуальные совмещения ребер, граней и даже кубов.