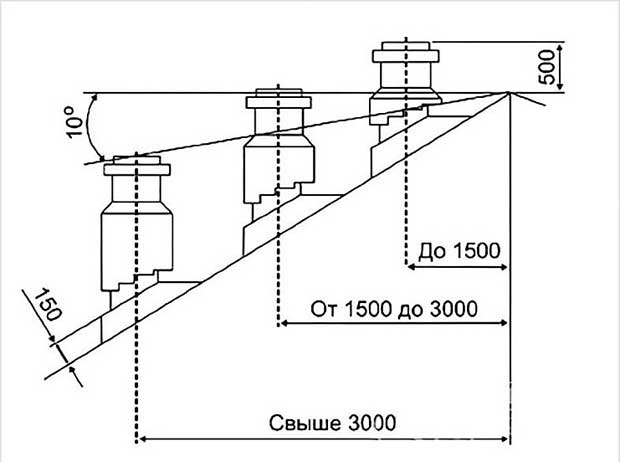
Расчёт уклонов

Выбор кровельного покрытия в зависимости от наклона крыши

На рынке материалы для крыши присутствуют в большом ассортименте, поэтому с выбором подходящего варианта особых проблем не будет. Кровельные покрытия отличаются по характеристикам и возможностям применения, и все их параметры необходимо изучить перед тем, как измерить угол крыши – только в этом случае удастся создать надежную и эффективную конструкцию.

Выбирая материал для кровли, стоит отталкиваться от следующих рекомендаций:

1. Если угол наклона стропил составляет от 2,5 до 10 градусов, то лучше всего подойдут покрытия из каменной крошки или гравия. В первом случае верхний слой покрытия имеет толщину 3-5 мм, а во втором – 10-15 мм.
2. При наклоне более 10 градусов оптимальным вариантом будут крупнозернистые или рулонные материалы, дополненные битумной гидроизоляцией.
3. Для обустройства скатных крыш с углом наклона не более 20 градусов обычно используется профнастил или листовой асбестоцемент. Все швы и стыки между кровельными материалами должны быть обработаны герметиком.
4. Если угол наклона крыши находится в пределах 20-60 градусов, то она чаще всего накрывается металлическими листами. Стыки материалов в данном случае нужно в обязательном порядке герметизировать.

Заключение

Знание того, как узнать угол наклона крыши в градусах, существенно упростит процесс ее проектирования и позволит создать максимально надежную конструкцию, которая сможет хорошо защищать коробку здания от атмосферных осадков, ветра и холода. 

Как рассчитать: нюансы

Чтобы вычислить оптимальный наклон двухскатной крыши (ее берем за основу как наиболее распространенную, практичную, эргономичную), необходимо знать следующие показатели:

• нагрузка от ветра в регионе;
• нагрузка от снега;
• пространство под крышей;
• какой материал используется для покрытия.

Нагрузка от ветра

Чтобы правильно рассчитать данный показатель, обратите внимание на карту ветровой нагрузки по регионам России. Чем выше класс (обозначен от I до VII), тем сильнее ветер в данной области

Карта ветровой нагрузки по регионам России поможет определить правильный угол наклона крыши

Отыщите на карте свой район. Если ветер очень сильный (классы V, VI, VII), то большой уклон не подходит. Такая система обладает большой парусностью. Данным термином строители описывают свойство конструкции принимать на себя ветер. Если он будет мощным, то крышу унесет. В ветреных районах нельзя делать кровлю с уклоном менее 30 градусов. Угол 25 градусов является недопустимым! Иначе ветер будет попадать под зазоры и материал, которым покрыта кровля, что приведет к порче конструкции.

Нагрузки от снега

Чтобы правильно рассчитать угол крыши, необходимо адекватно понимать нагрузку от снега, которую кровля будет испытывать в холодное время года.

Если вы живете на Севере, то на один квадратный метр в январе-феврале приходится около 400 килограммов снега.

Если вы проживаете в регионе, где не только часто идут снегопады, но при этом дуют сильные ветра, то угол надо уменьшить до 35 градусов. Почему не сделать наклон, наоборот, больше, чтобы снег не задерживался совсем? Это нерационально, поскольку в таком случае кратно вырастет нагрузка на стены и фундамент, а также ваш бюджет (понадобятся дополнительные доски, балки).

Пространство под крышей

Обустройство жилой комнаты под самой кровлей возможно только при двускатной или многоскатной конструкциях. Если речь идет об односкатной или плоской крыше, то находиться под ней будет нереально.

Обработать внутреннее покрытие крыши можно короедом. Так материал дольше сохранит свою прочность.

Решили обустроить чердак? Позаботьтесь о внутреннем утеплении.

Внешнее покрытие

Угол наклона в градусах зависит и от типа материала, который используют для внешнего покрытия:

• шифер кладут под углом не менее 20 градусов: если меньше, то вода попадет в щели между единицами материала;
• металлочерепица – от 15, иначе ветер снесет покрытие;
• профнастил – не менее 10;
• битум – до 15. Чем больше угол, тем больше вероятность, что битум сползет вниз, особенно в жару;
• рулонный материал – до 25.

Расчет угла, если заданы три точки в прямоугольной системе координат

В этом случае проще будет разобраться с объяснениями сразу на примере.

Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между \(\overrightarrow{AC}\) и \(\overrightarrow{BC}\).

Решение

Для начала найдем их координаты по известным координатам заданных точек:

\(\overrightarrow{AC}=(6-3, -1-(-2))=(3,1)\)

\(\overrightarrow{BC}=(6-2, -1-1)=(4,-2)\)

После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:

\(\cos\left(\widehat{\overrightarrow{AC};\overrightarrow{BC}}\right)=\frac{(\overrightarrow{AC};\;\overrightarrow{BC})}{\left|\overrightarrow{AC}\right|\cdot\left|\overrightarrow{BC}\right|}=\frac{3\cdot4+1\cdot(-2)}{\sqrt{3^2+1^2}\cdot\sqrt{4^2+{(-2)}^2}}=\frac{10}{\sqrt{10}\cdot2\sqrt5}=\frac{10}{10\sqrt2}=\frac1{\sqrt2}\)

Ответ: \(\cos\left(\widehat{\overrightarrow{AC};\overrightarrow{BC}}\right)=\frac1{\sqrt2}.\)

Угол наклона в зависимости от кровельного материала

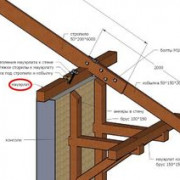
Крыша на доме может иметь практически любой вид — может иметь низкие скаты, может — почти отвесные

Важно при этом правильно рассчитать ее параметры — сечение стропильных ног и шаг их установки

Если вы хотите уложить на крышу определенный вид кровельного материала, принимать во внимание надо такой показатель, как максимальный и минимальный угол наклона для данного материала

Наименование кровельного материала

Минимальный угол наклона (в градусах)

Минимальные углы прописаны в ГОСТе (смотрите таблицу выше), но часто производители дают свои рекомендации, так что желательно определиться с конкретной маркой еще на стадии проектирования.

Чаще угол ската крыши часто определяют исходя из того, как сделаны они у соседей. С практической точки зрения это правильно — условия у близлежащих домов аналогичны, и, если соседские крыши стоят хорошо, не текут, можно взять за основу их параметры. Если же по соседству нет крыш с тем кровельным материалом, который вы планируете использовать, можно начать расчеты со средних значений. Они приведены в следующей таблице.

Тип кровлеьного материала

Рекомендуемый угол наклона минимальный/максимальный

Какой наклон ската делают чаще всего

Как видите, в графе «как делают» в большинстве случаев есть солидный диапазон. Так что имеется возможность варьировать внешний вид здания даже с одинаковой крышей. Ведь кроме практической роли крыша еще и украшение. И при выборе угла ее наклона немаловажную роль играет эстетическая составляющая. Сделать это проще в программах, дающих возможность отобразить объект в объемном изображении. Если воспользоваться этой методикой, то рассчитать угол наклона крыши в данном случае — выбрать его из определенного диапазона.

Уклон в процентах

Уклоны в градусах и процентах 1º — 1,7 % 1 % — 34′ 20″ Просто для справки.

вы бы не позорились, утверждать что величина уклона прямо и линейно пропорциональна углу — это просто незнание основ математики! или просто дезинформация! «по секрету»: уклон — это отношение противолежащего катета к прилежащему — в математике называют «тангенс угла», теперь откройте учебник и посмотрите график этой функции — как видите, он совсем не похож на прямую линию.

Даже простейший пример: угол 45º. а уклон = 100% — это уже в вашу формулу не вписывается. или вы считаете что при 45º катеты не равны ?

в некоторых документах увидел что этот уклон пишут намного больше, с чем это связано?

так может с тем и связано — что уклон в некоторых случаях намного больше! у нас например некоторые и уклон скатной кровли до сих пор пишут в долях, а не в градусах. так что если сравнивать уклон в долях для дороги и уклон для ската кровли — разница может быть огромной, но в этом нет ошибки.

Наклон канализации в частном доме – делаем своими руками

Современный частный дом принято оборудовать системой слива. Даже если магистраль городской канализации находится на значительном отдалении, устанавливаются септики или оборудуются специальные емкости для их накопления.

Для монтажа внутренней сети применяются те же материалы и  элементы. Теми же остаются и нормы уклона вне жилого дома.

Для наружного контура канализации в частном доме можно использовать трубы размером 100 миллиметров, а при небольшом количестве живущих в доме людей, возможно и применение 80-ти миллиметровых.

Трубопровод протягивается по траншее с глубиной заложения не менее уровня промерзания грунта. Если это покажется чрезмерным (для Подмосковья этот показатель составляет 1,8 метра), можно установить менее глубокую утепленную магистраль или установить на сливной трубопровод греющий кабель с автоматикой включения при понижении температуры грунта ниже нуля градусов.

Требования по углу наклона в частном доме подчиняются тем же нормативам, что и для других устройств.

Все работы по устройству системы слива при загородном доме могут быть выполнены следующим образом:

1. Определить нужные параметры трубопровода для внутренней и наружной сливных систем.
2. Выполнить эскизный проект трубопровода с указанием привязки к горизонту на различных уровнях.
3. Произвести монтаж внутренней канализационной сети с выполнением требований СНиПа. Вывод разводки из внутренних помещений произвести через короткий стояк размером 80 или 100 миллиметров. Стояк через угловой переход впоследствии соединить с наружной частью канализации.
4. Отрыть траншею для прокладки наружной части. При этом нужно учитывать глубину промерзания грунта, если трубопровод не по проекту утепляется. Глубина траншеи выбирается с учетом последующей подсыпки
5. На дно траншеи насыпать слой песка толщиной 15-20 сантиметров, утрамбовать и пролить водой для лучшего уплотнения. Уровень дна траншеи при копке и песчаной подсыпки по отношению к горизонту контролировать с использованием водяного уровня.
6. Установить на песчаную подсыпку опоры для трубопровода. Для этого можно использовать бетонные блоки или кирпичи. При установке нужно руководствоваться требованием по уклону канализационной трубы 110 миллиметров. Количество опор зависит от длины траншей, а расстояние между ними допускается не более метра. Это связано с тем, что на трубу будет оказываться давление от грунта, которым впоследствии зарывается траншея.
7. После укладки трубы на опоры необходимо проверить работоспособность системы пробным пропуском воды по ней. Если выполнено требование наклона канализационной трубы 100 мм и вода проходит по ней без протечек, можно приступать к закрытию траншеи. Сначала трубопровод аккуратно засыпается слоем песка с его трамбовкой по бокам и поверх нее. Закрыв все полностью, производят засыпку траншеи ранее вынутым грунтом и рекультивацию верхнего слоя почвы.
8. При устройстве сложно разветвленной канализационной схемы слива на участке, когда имеются дополнительные источники стоков, используются те же правила по наклону трубы для канализации в частном доме. Но возникает необходимость в устройстве смотровых колодцев в месте пересечения двух или более систем. В таком варианте глубина размещения в месте стыковки согласуется с этим фактором для основной схемы, которая выводит стоки во внешнее пространство.

Смотреть видео

Если вблизи дома проходит ветвь городской канализации, желательно подключить свой сток именно к ней. Для этого придется получить разрешение от Горводоканала, ведающего системой, понеся при этом определенные затраты. Но при таком случае впоследствии не понадобятся расходы на очистку септика или выгребной ямы.

Единицы измерения и инструменты

В основание металлической конструкции встроены цифровой дисплей с элементами управления.

Величина уклона на всех чертежах может обозначаться в градусах или в процентах, а сам он обозначается буквой «i». В настоящий момент нет строгих правил, как обозначать данную величину. Единицей измерения считают градусы или проценты (%).

Угол уклона измеряется двумя способами:

1. Специальным уклономером.
2. Математическим способом, с помощью вычислений.

Уклономер — это специальная рейка с рамкой, у которой между планками есть ось, на которой закреплен маятник, и своя шкала деления. Когда эта рейка расположена в горизонтальном положении, то маятник на ее шкале отклонен на ноль градусов. Для произведения измерения уклона ската рейку прибора располагают перпендикулярно коньку, в вертикальном положении.

По шкале определяют угол отклонения маятника, который указывает уклон этого ската данной крыши в градусах. Этот метод определения применяется очень и очень редко. На данный момент разработано множество геодезических приборов для определения этих величин и специальные уровни-уклономеры, как капельные, так и электронные.

Можно спокойно рассчитать наклон данной крыши, не прибегая к использованию специальных геодезических, механических и других видов приборов для замеров уклона. Необходимо просто измерить некоторые параметры крыши:

1. Вертикальная высота (обозначается как H) — высота от верхней точки данного ската (обычно считают от конька) до самой нижней точки (так называемого карниза).
2. Заложение — горизонтальный промежуток от самой нижней точки данного ската до самой верхней его точки.

Уклон крыши (его величину) с применением математического расчета находят так.

Угол наклона отдельного ската i выражается через отношение измеренной высоты крыши Н к расстоянию заложения L. Таким образом

Для точного определения этого значения в процентах отношение i умножают на 100. Затем, для определения его значения в градусах, мы производим перевод процентов в градусы.

Для полного понимания этого метода приведем наглядный расчет:

высота равна 3,0 м,

длина заложения равна 5 м.

По формуле вычисляем i:

Расчет угла, если вектор задан координатами

В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде \(\overrightarrow a=\left(a_x;a_y\right)\) и \(\overrightarrow b=\left(b_x;b_y\right)\), то угол между ними можно найти следующим образом:

\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y}{\sqrt{a_x^2+a_y^2}\cdot\sqrt{b_x^2+b_y^2}}\)

Если же координаты находятся в трехмерном пространстве и заданы в виде:

\(\overrightarrow a=\left(a_x;a_y;a_z\right)\)

\( \overrightarrow b=\left(b_x;b_y;b_z\right)\)

то формула принимает такой вид:

\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z}{\sqrt{a_x^2+a_y^2+a_z^2}\cdot\sqrt{b_x^2+b_y^2+b_z^2}}\)

Какой кровельный материал выбрать

Кровельные покрытия различаются по структуре, прочности, ценовому диапазону. Все же наиболее важным критерием выбора материала является его структура. Чем шершавее поверхность, тем дольше осадки будут задерживаться на крыше.

Существуют несколько типов кровельного материала, который влияет на определение величины наклона.

1. Кровля из рулонных битумных материалов используется при минимальном уклоне крыши от 0 до 3 °. Рулонная кровля достаточно проста в использовании и имеет несколько плюсов: гибкость, прочность, теплоизоляция.
2. При уклоне крыши от 4 ° применяется фальцевая кровля, которая обладает повышенной степенью износостойкости и прочности. Это обусловлено тем, что данный материал состоит из полимеров.
3. Шиферное покрытие принято использовать от 9 °.
4. Различные виды черепицы (керамическая, битумная, металлическая и цементно-песчаная) применяются, если угол наклона превышает 11 °. Черепица, в частности металлическая, является одним из самых популярных видов кровли на сегодняшний день, так как ее применение возможно в различных климатических условиях.
5. Свыше 39 ° обычно используется деревянная кровля, однако такой материал требует к себе постоянного внимания и должного ухода.

Для того чтобы ваша крыша была построена правильно и прослужила долгое время, не обязательно обращаться к услугам специалистов. Достаточно грамотно рассчитать угол наклона ската и подобрать подходящий материал.

Посмотрите видео и узнайте, какой должен быть у крыши

При создании проектной документации очень часто уклон обозначается не в градусах, а в процентах. Это позволяет избежать проблем с монтажом готовой конструкции.

Уклон в градусах рассчитывается для крутых скатов крыш, так будет удобнее. Но когда речь идет о небольшом угле, то использование процентов для обозначения значения уклона поможет избежать ошибок при расчете и монтаже.

Чтобы узнать процентное значение уклона на земельном участке, можно воспользоваться следующими методами:

• самым простым и точным способом определения угла склона будет нивелирование. При помощи специального прибора измеряются все необходимые величины и путем простого соотношения производятся несложные вычисления. Разность высот делится на расстояние, затем результат умножается на 100%. Современные нивелиры оснащены встроенной памятью, которая значительно облегчает работу замерщиков;
• измерить уклон можно и на своем участке без использования дорогостоящего оборудования. На плане участка или топографических картах часто обозначаются высоты. На земельном участке эти места намечаются, можно использовать для этой цели колышки, затем расстояние между ними измеряется землемерным циркулем. Математические расчеты производятся по той же схеме, что и при работе с нивелиром;
• используя метод интерполирования, значение уклона в процентах, можно вычислить по топографической карте. Для этого также определяется разность отметок, которая делится на расстояние и умножается на 100%.

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Катет a = Катет b = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

c = a/_cos(β) = b/_cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

c = a/_sin(α) = b/_sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Гипотенуза c = Катет _{(известный)} = Катет _{(искомый)} =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

a = √c² — b²

b = √c² — a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² — 4² = √25 — 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Гипотенуза c = Угол (прилежащий катету) = °Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Гипотенуза c = Угол (противолежащий катету) = °Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Катет (известный) = Угол (прилежащий известному катету) = °Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Катет (известный) = Угол (противолежащий известному катету) = °Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см

Вы здесь

Онлайн калькулятор — Учеба и наука — Математика — Геометрия — Геометрический калькулятор — Треугольник

Треугольник

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Зная: Стороны треугольника	Зная: Два угла и сторону треугольника	Зная: Два угла и сторону треугольника «A»
Зная: Две стороны и угол треугольника	Прямоугольный треугольник	Зная: Катет и гипотенуза прямоугольного треугольника
Катет «B» и гипотенуза прямоугольного треугольника	Зная: Катет и угол прямоугольного треугольника	Катет «A» и угол «β» прямоугольного треугольника
Катет «B» и угол «α» прямоугольного треугольника	Катет «B» и угол «β» прямоугольного треугольника	Зная: Гипотенузу и угол прямоугольного треугольника
Гипотенуза и угол «β» прямоугольного треугольника	Равнобедренный треугольник	Зная: Высоту и сторону равнобедренного треугольника
Высота и сторона «B» равнобедренного треугольника	Зная: Сторону и угол равнобедренного треугольника	Сторона «A» и угол «β» равнобедренного треугольника
Сторона «B» и угол «α» равнобедренного треугольника	Сторона «B» и угол «β» равнобедренного треугольника	Зная: Высоту и угол равнобедренного треугольника
Высота и угол «β» равнобедренного треугольника	Равносторонний треугольник	Зная: Площадь равностороннего треугольника
Зная: Высоту равностороннего треугольника	Зная: Радиус вписанной окр. равностороннего треугольника	Зная: Радиус описанной окр. равностороннего треугольника
Зная: Основание и высоту треугольника

Признаки равенства прямоугольных треугольников

1. Признак равенства прямоугольных треугольников по двум катетам

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то эти треугольники равны.

Действительно. Пусть , (Рис.3). Поскольку , то по первому признаку равенства треугольников следует, что треугольники и равны.

2. Признак равенства прямоугольных треугольников по катету и прилежащему к нему острому углу

Если катет и прилежащий к нему острый угол прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Действительно. Так как , , (Рис.4), то из второго признака равенства треугольников следует, что треугольники и равны.

Теорема 1. Если гипотенуза и прилежащий к нему острый угол прямоугольного треугольника соответственно равны гипотенузе и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Доказательство. Пусть и (Рис.5). Так как данные треугольники прямоугольные, то имеет место также равенство . Тогда из второго признака равенства треугольников следует, что треугольники и равны.

4. Признак равенства прямоугольных треугольников по гипотенузе и катету

Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Доказательство. Рассмотрим треугольники и , где , и углы C и C₁ прямые (Рис.6).

Поскольку , , , то треугольник можно наложить на треугольник так, чтобы вершина C совместилась с верншиной C₁ а стороны CA и CB наложились на лучи C₁A₁ и C₁B₁, соответственно (Рис.7).

Так как CB=C₁B₁, то вершина B совместится с вершиной B₁. Покажем, теперь, что вершина A совместится с вершиной A₁. Предположим, что они не совместятся. Тогда получим равнобедренный треугольник ABA₁, поскольку AB=A₁B₁. Но в этом случае . Но как мы видим из Рис.7 угол , острый а угол тупой (так как он является смежанным углом к острому углу BAC), что невозможно. Следовательно вершина A совместится с вершиной A₁.